Hermite-Gauss mode conversion

Introduction

Arbitrary solutions of the paraxial Helmholtz equation can be expressed as combinations of Hermite-Gaussian modes (whose amplitude profiles are separable in x and y using Cartesian coordinates).

For many applications, it is useful to convert the fundamental laser mode TEM00 to a higher order of Hermite-Gaussian beams:

Phase ElementOutput IntensityPhase ElementOutput Intensity
TEM00 TEM20
TEM01 TEM12
TEM10 TEM21
TEM11 TEM22
TEM02

Each mode HGlm is denoted by two indices, l & m, which represent the number of modes in the x & y directions, respectively.

Typical Applications

  • Communication
  • Scientific & research
  • Scanning applications
  • STED microscopy
  • Optical tweezing
  • Optical trapping

Feature

  • Aberration free
  • High efficiency
 

Typical Optical set-up:

Laser Setup lowres

Typical Operating Principle

The operating principle is quite straight-forward – a Fourier Transform (FT) is applied on the initial field amplitude and phase to obtain the desired field (or intensity) at far-field. In this way, the fundamental Gaussian beam TEM_00 is converted to a higher order of Hermite-Gaussian modes. For example – conversion of TEM_00 to TEM_10:

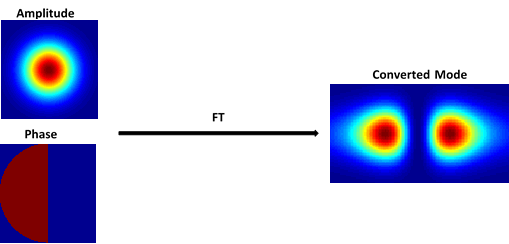
mode converter - Operating Principle

For the phase-plate element, the height of the step is defined as: 

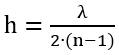
step height

where n is the refractive index of the material.

Design Considerations:

For a high-quality performance, the laser output should be Single Mode (TEM00 with an M2 value <1.3. If the M2 is larger, it may still be possible to reduce the M2 value by inserting a spatial filter in between the laser and the DOE lens component. 

All optics in the beam path should be of high quality, i.e. have a low irregularity figure, in order not to introdcue wav-front errors which would degrade the diffractive phase element’s performance.

General Specifications:

Materials:Fused Silica, Sapphire, ZnSe, Plastics
Wavelength range:193[nm] to 10.6[μm]
DOE design:Binary (2-level)
Element size:Few mm to 100 [mm]
Coating (optional):AR/AR Coating
Custom Design:Available

π Phase-Plate

Introduction:

For many applications, it is necessary to use a phase element with a π-phase at the center. For imaging purposes using this element will result in an increased depth-of-focus, and for particle manipulation purpose, using this element will result in optical tweezing\trapping.

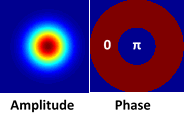
mode converters - Pi phase plate

Standard Products:

Part NumberDiameter [mm]Aperture size [mm]MaterialDescriptionAdd to Quote
PE-20225.423.6 Fused SilicaHalf-space π difference mode converter, TEM01 (or TEM10) Add to Quote
PE-23025.423.6 Fused SilicaQuarter-space π difference mode converter, TEM11 Add to Quote
PE-215119.2Fused SilicaRound π phase at the center, diameter 4817 μm Add to Quote
PE-21623.69.2Fused SilicaRound π phase at the center, diameter 5680 μm Add to Quote
PE-2172023.6 Fused SilicaRound π phase at the center, diameter 6200 μm Add to Quote
PE-21825.4 18.2Fused SilicaRound π phase at the center, diameter 8428 μm Add to Quote
PE-21925.4 23.6Fused SilicaRound π phase at the center, diameter 10838 μm Add to Quote
PE-22025.4 23.6Fused SilicaRound π phase at the center, diameter 7224 μm Add to Quote
PE-221119.2Fused SilicaRound π phase at the center, diameter 3612 μm Add to Quote
PE-222119.2Fused Silica Round π phase at the center, diameter 4214 μm Add to Quote
PE-223119.2Fused Silica Round π phase at the center, diameter 3000 μm Add to Quote
PE-224119.2Fused SilicaRound π phase at the center, diameter 5400 μm Add to Quote
PE-22525.423.6Fused SilicaRound π phase at the center, diameter 6384 μm Add to Quote
PE-22612.5 10.7Fused SilicaRound π phase at the center, diameter 6840 μm Add to Quote
PE-22725.423.6Fused SilicaRound π phase at the center, diameter 8900 μm Add to Quote
PE-228119.2Fused SilicaRound π phase at the center, diameter 1200 μm Add to Quote
PE-229119.2Fused SilicaRound π phase at the center, diameter 1800 μm Add to Quote
PE-24125.422.9Fused SilicaRound π phase at the center, diameter 3860 μm Add to Quote

For a quotation of an above Part Number, please specify the wavelength used.

Contact us for more information or for a custom solution.

References: